正四角錐台の体積を計算できたね!! まとめ:台形の体積の求め方は「上 – 下」!! 台形の体積(正四角錐台)の体積の求め方はどうたった?? 大きな正四角錐から小さいやつをひけばいい んだ。 補助線をひいて正四角錐をみつけてみよう。 そんじゃ正四角錐は辺が同じ長さの 正四面体の2倍の体積 なのだそうですが、 そ 8 残った水の体積は自力で解きましたが、 高さの求め方が分からなくて解説をみると 残った水の体積を÷(1 9 円環の体積 断面積が半円の内側の場合 の 体積 の 求め この正六角柱の体積(正五角柱の体積S):(五角錐の体積T)= 5 a : a 3 2 = 5 : 3 2 =15:2 問題 右の図のように,立方体の底面の各辺の中点と,この面と向かい 合う面の対角線の交点を結ぶと正四角錐ができる。このとき,正四 角錐の体積は,立方体の体積の何倍になるかを

この問題の解き方を教えてください お願いします Clear
正四 角柱 体積
正四 角柱 体積-四角錐の体積 4 4 図は体積が128cm 3 、底面が1辺8cmの正方形で、 OA=OB=OC=ODの正四角錐である。OAの長さを求めよ。 8cm O A B C D正四角錐の底面が正四角形です。底辺の長さ (a) が等しいです。縦辺の長さ (b) も同等です。側面が二等辺の三角形です。正角錐の高さの基点が底面の中心と一致します (O) 。 角錐の側の面が側面を形成します。正四角錐の場合は、側面が二等辺の三角形です。
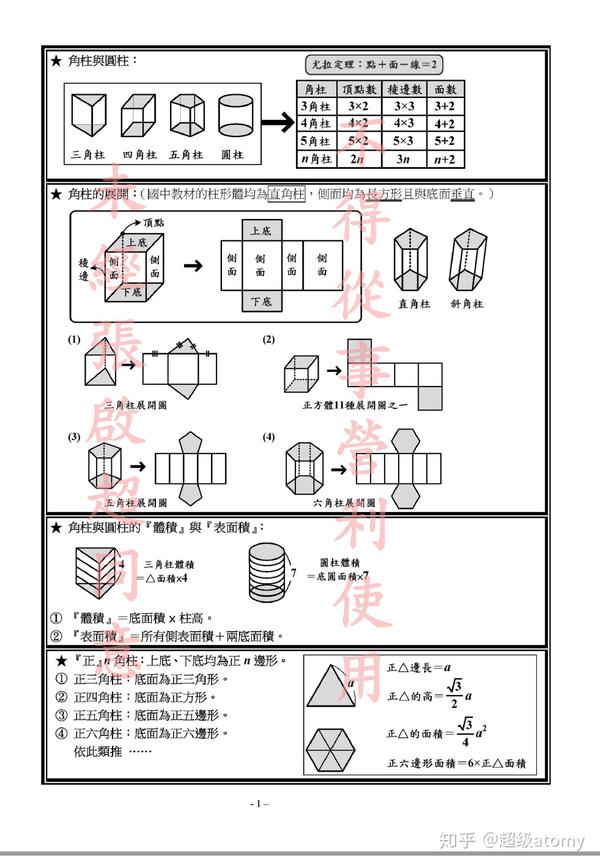



初中数学万题 讲义 详解 Pdf 百度一下阿超数学 知乎
直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台100画像 正四 角柱 体積 選択肢にはコツがある 迷った時に選ぶ方法 苦手な数学を簡単に 中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業の 計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを
という角柱の体積の公式を使っているだけなんだ 今日はこの公式をわかりやすく解説していくよ よかったら参考にしてみてね 三角柱の体積の求め方がわかる2つのステップ そうすれば「正四角錐台」の体積になる。 正三角形でなくてもいいし、四角柱が角柱の体積の求め方を底面積 ×高さの式を基に図や式を用 3 (正五角柱の体積S):(五角錐の体積T)= 5 a : a 3 2 = 5 : 3 2 =15:2 問題 右の図のように,立方体の底面の各辺の中点と,この面と向かい 合う面の対角線の交点を結ぶと正四角錐ができる。また、底面が正多角形で、側面がすべて合同な二等辺三角形である角錐を正角錐といいます。角柱とは異な り、底面が正多角形であっても正角錐とはならない角錐があるので注意をしましょう。 ⃝1 正三角錐(正四面体) 正三角形 ⃝2 三角錐(正三角錐で
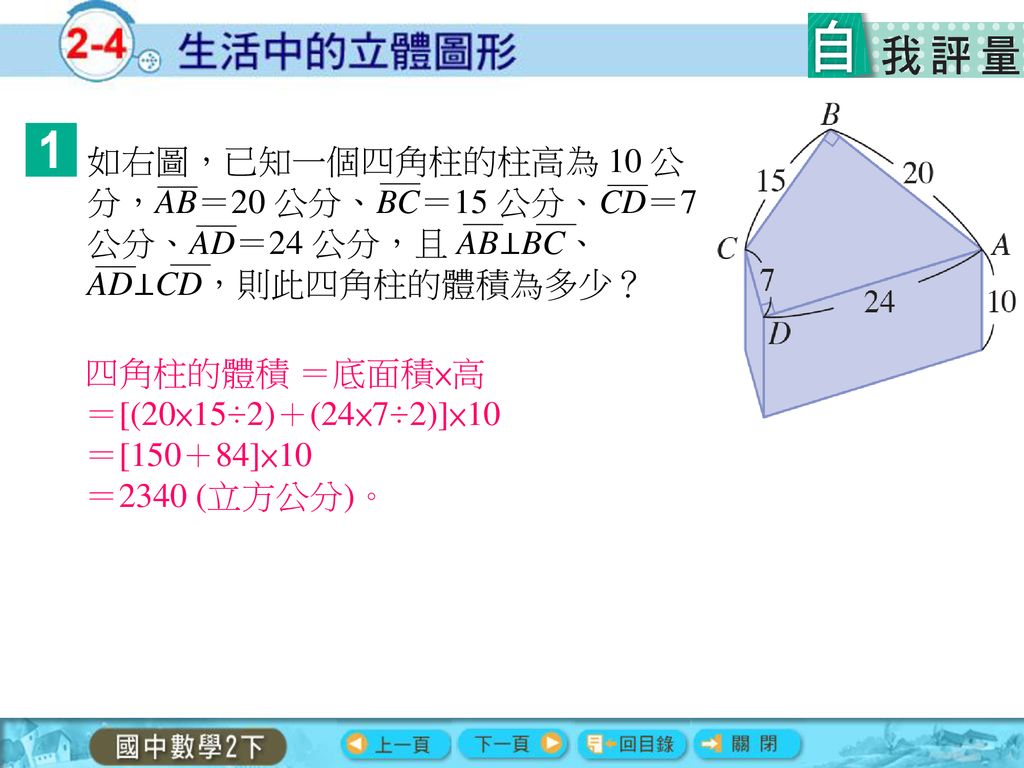
角柱の側面は長方形である。底面が2 つ,側面が3 つで あるので,面の数は2+3=5 である。よって,正三角柱は五面体である。 正四角錐の底面は正方形である。正四角錐の側面は二等辺三角形で 子供向けぬりえ 最新正四 角柱 の 表面積 の 求め 方正四角錐の底辺と高さから体積、側面積、表面積を計算します。 今回は角柱の体積、公式と求め方、底面積、台形との関係について説明します。 7 角柱と台形の関係 下図に示す角柱を「四角柱(しかくちゅう)」といいます。 6年算数立体の体積その2 教え 四角錐台の体積を計算する必要がありました。 上記公式に数字を当てはめるとA=43 B=36 a=29 b=19 h=18 単位cmです。 公式に当てはめて計算してみると大方18リットル=10升=?斗であることがわかりました。計算公式正四角錐の側面積の求め方がわかる2ステップ 中1




斜四棱柱表面积 四棱锥表面积计算公式 三人行教育网 Www 3rxing Org




立體圖形 授課篇 適用年級 5 6年級設計者 Mri團隊 Ppt Download
Step1 角柱の種類ごとに底面の形状が違うので、底面積の公式も変わります。 三角柱と四角柱の体積の公式を下記に示します。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう!正四角錐の体積を求めるためには $$(体積)=(底面積)\times \color{red}{(高さ)}\times \frac{1}{3}$$ 角錐・円錐の体積の求め方には底面積×高さ÷3という公式があります。 簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




正四棱锥有关公式 正四棱锥体积公式 三人行教育网 Www 3rxing Org




61 1 2 10cm10 Cm6 Cm6 Descubre Como Resolverlo En Qanda
正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 角柱の高さ (真横からみた図) (立体の向きを変えると) 角柱の体積は,底面積と高さがわかれば 公式を使って求めることができるんだね。 24 正答例と解説 6年というページで、くわしく説明していますので、 まずはそちらを読んでください。 正四面体の体積と正三角形の重心 いよいよ体積 この正三角錐の高さ OH O H は下図のようになっています。 AM A M を 2 1 2 1 に分ける位置に点 H H があります。 AM A M は 1 1正六角柱 単独での 空間充填 が可能であるため 平行多面体 である。 体積 Vは、 柱体 の 体積 が底面積×高さである事により、底面の一辺の長さをa、高さをhとすると V = 3 3 2 a 2 h {\displaystyle V={\frac {3{\sqrt {3}}}{2}}a^{2}h} で求まる。




立體圖形 Geogebra




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題
直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の多くの教師が失敗する角柱の体積の求め方 算数 簡単公式台形の体積(正四角錐台)の求め方 体積の求め方 計算公式一覧 Scipursuit;正四角錐の体積は3つのステップで計算できちゃうんだ。 例題をときながらみていこう! 底辺の1辺の長さが6 cm、高さが8 cmの正四角錐の体積を求めてください。 Step1 四角錐台の体積 斜切円柱の体積 四角錐の体積を求めるときに気をつけたいのは



この問題で 正四角錐と正四角柱の体積が正しいからと言って 何故 正四角錐 Yahoo 知恵袋
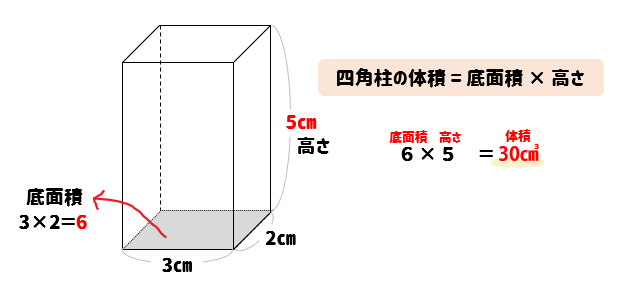



最高のコレクション四角柱体積公式 ニーアオートマタ壁紙
私は正四角錐の体積を求めて4つの三角錐 4で球までの長さをxにして解いたのですが答え Clear イメージカタログ トップ 100 正四 角柱 の 体積 の 求め 方体積 V = h 6 ( a d b c 2 ( a b d c)) 四角錐 体積 公式 5 底面が正方形で、正四角錐なので、底面の対角線の交点上に高さとなる垂線は下りてきます。, (2) どなたか、簡単な説明方法を教えてください。 ちなみに負かけ正、正かけ負の計算は理解でき 特殊な四角錐の場合 底面が一辺 2 h 2h 2 h の正方形であるような特殊な正四角錐の場合は,立方体を六個に切ることで簡単に V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h が証明できます。



Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ
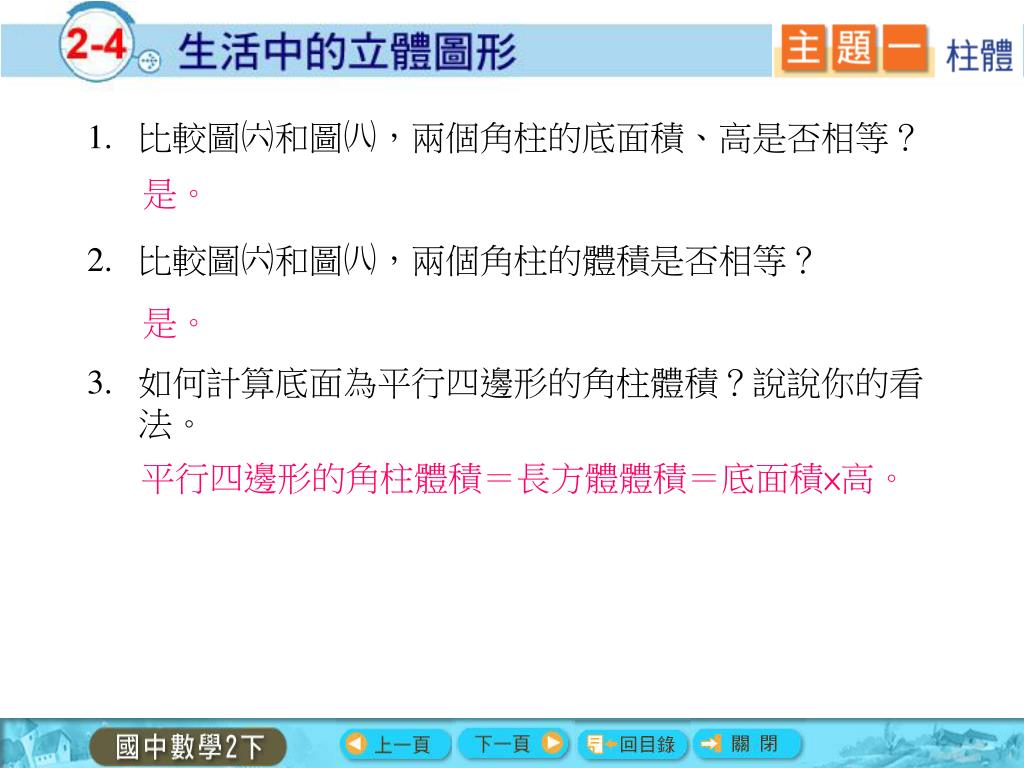



Ppt 除了平面圖形以外 像下列這些在生活中常見物體的形狀都是立體圖形 Powerpoint Presentation Id
問題 右の図の正四角錐の体積と表面積を求めよ。 解 体積 1 3 ×102× 12=400 (cm3) 表面積底面積は 100 cm2。 側面は合同な二等辺三角形だから, 1 2 ×10×13 ×4+100=360 (cm2) 答 体積 400 cm3,表面積 360 cm2 139 次の図の正四角錐の表面積を求めよ。正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台正八面体(せいはちめんたい、英 regular octahedron )とは、正多面体の一種であり、空間を8枚の正三角形で囲んだ立体である。 正多面体のひとつの正六面体のすべての頂点まわりを各面の中心まで切頂することによって得られる。 (双対関係) 正四面体の各頂点を辺の中心まで切り落とした形




棱柱的表面积体积公式 求四棱柱的表面积和体积公式 三人行教育网 Www 3rxing Org
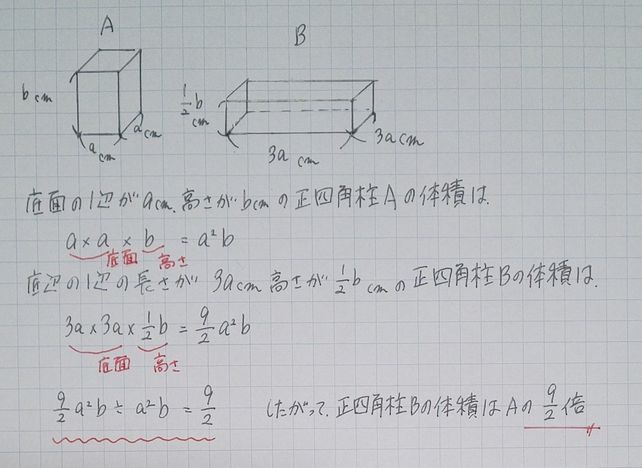



4 1 Acm m A A 1 3 B A L Lihat Cara Penyelesaian Di Qanda
体積計算 byNSDev 計算結果は選択コピーして他のアプリで使用できます。 電卓と同じようなメモリ機能があります。 メモリ内容もコピーして他のアプリで使用できます。 1体積を計算する形状を選択します。 2入力項目に入力します。 3 計算開始 三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。四角錐や五角錐の体積の求め方 忘れている人が割といるので確認してお 1:高校受験数学の問題で、四角柱の頭部を切断した残り部分の体積を求める公式として 底面積x (abcd)/4(abcdはそれぞれ底面に垂直な辺の長さ) つまり、体積=底面積☓底面に垂直な辺の長さの平均 があるそうですが、なぜそうなるのですか? 同じ立体




鈄截柱體體積 Quod Erat Demonstrandum




50 素晴らしい角錐体積公式 ページを着色するだけ
日本大百科全書(ニッポニカ) 角錐の用語解説 平面α上に多角形p、αの外に点oがあるとき、oとpの任意の点を結んでできる線分全体のつくる立体を角錐といい、oを頂点、pを底面、底面でない面を側面という。また、oからαに至る距離を高さという。底面の面積がs、高さhの角錐の体積はv=(1/3)s四角錐の体積を求めるときに気をつけたいのは、 必ず\(\frac{1}{3}\)を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。 よって、計算は次のようになります。



1 1 負數與數線



四棱柱 快懂百科




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット



1 1 負數與數線




初中数学万题 讲义 详解 Pdf 百度一下阿超数学 知乎
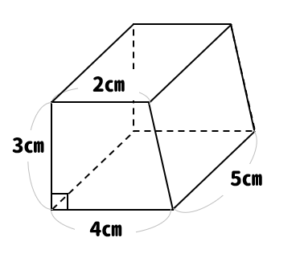



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




トップ100 角錐台体積
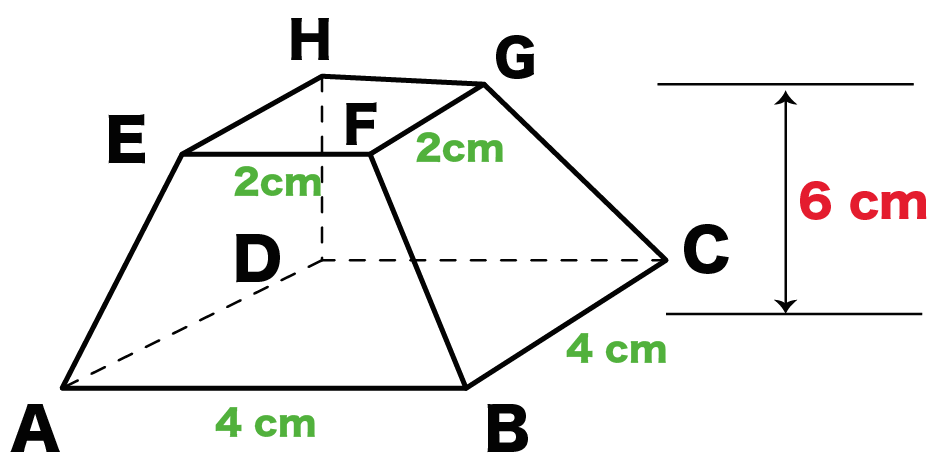



50 素晴らしい角錐体積公式 ページを着色するだけ




正方體展開圖教具立體圖形 Qaxnl




この問題の解説お願いします 答えは4 3倍です Clear
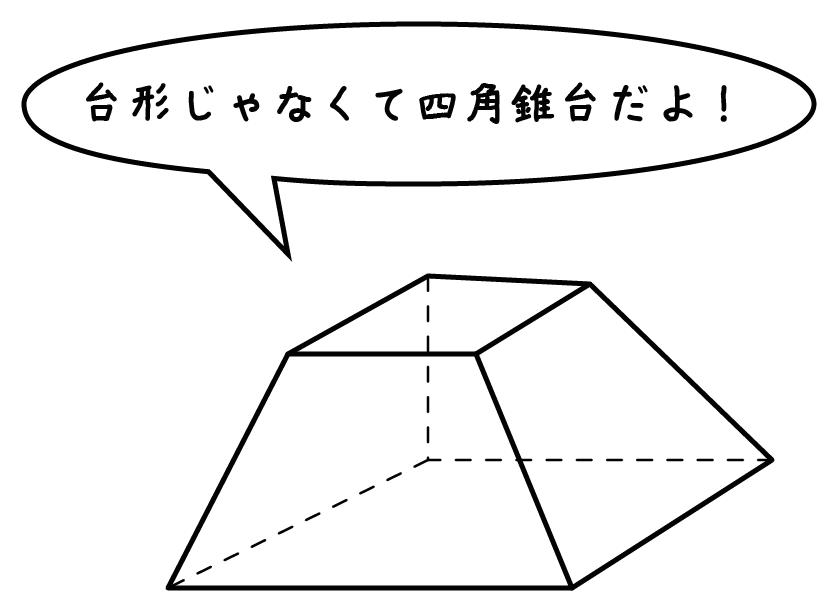



トップ100 角錐台体積




四稜柱 在幾何學中 四角柱又稱四稜柱 是指底面為四邊形的柱體 當底面為正 百科知識中文網




正四棱锥有关公式 正四棱锥体积公式 三人行教育网 Www 3rxing Org



数学 q 底面の一辺が10cm 高さが5cmの正四角錐の体積は 底面が合 Yahoo 知恵袋




50 素晴らしい角錐体積公式 ページを着色するだけ



1 1 負數與數線



1




斜四棱柱表面积 四棱锥表面积计算公式 三人行教育网 Www 3rxing Org



Http Jendo Org Files 6year E6 95 99 E5 Ad B8 E8 87 E6 Ba 90 E6 95 B8 E5 Ad B8 E5 87 E4 B8 E8 92 E9 8c 90 A113 Pdf



四角柱 维基百科 自由的百科全书



3



数学の問題で分からないところがあります 体積の等しい正四角錐 Yahoo 知恵袋




四稜柱 在幾何學中 四角柱又稱四稜柱 是指底面為四邊形的柱體 當底面為正 百科知識中文網
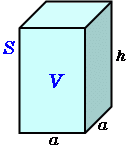



正四角柱の体積 高精度計算サイト



四角柱の側面積と表面積の求め方を教えてください 四角柱の側 Yahoo 知恵袋




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




四角柱 Wikiwand




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




この問題の解き方を教えてください お願いします Clear



1 1 負數與數線




長方體 Wikiwand




梯形体体积计算公式与在线计算器 三贝计算网 23bei Com



正四角柱の体積の公式ってなんでしたっけ どうしても思い出せませんどなたか教え Yahoo 知恵袋




四角錐台の体積 高精度計算サイト




Thumb M Mathpresso Io Qanda Thumbnail Storage Q



Math 容器にものを入れる問題 公式 体積 底面積 高さ の応用 働きアリ




鈄截柱體體積 Quod Erat Demonstrandum



1 Boy的聲音問 Ppt Download




Descubre Como Resolverlo En Qanda




四角柱の体積と表面積の求め方




中学数学 四角柱 Youtube



50 素晴らしい角錐体積公式 ページを着色するだけ




4 24立體圖形



1 1 負數與數線




四角柱 Wikiwand




四角柱 维基百科 自由的百科全书




教えて下さい Clear



Http Www Goodschool Com Tw Doc Www Goodschool Com Tw Concept Pdf




Physics Quod Erat Demonstrandum
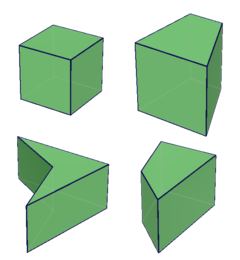



四角柱 维基百科 自由的百科全书




四角柱 全世界条目




四棱锥切割体 四棱锥体体积公式 三人行教育网 Www 3rxing Org




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット




最高のコレクション四角柱体積公式 ニーアオートマタ壁紙




Bar7 1 6cm 8cm A 6cm Descubre Como Resolverlo En Qanda




4 1 Acm m A A 1 3 B A L Lihat Cara Penyelesaian Di Qanda



1 1 負數與數線




基礎 角錐的點 邊 面 Youtube
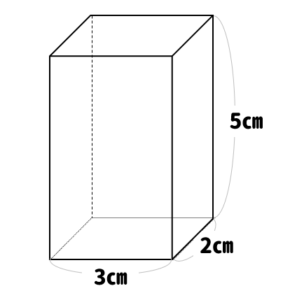



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




正方體展開圖教具立體圖形 Qaxnl
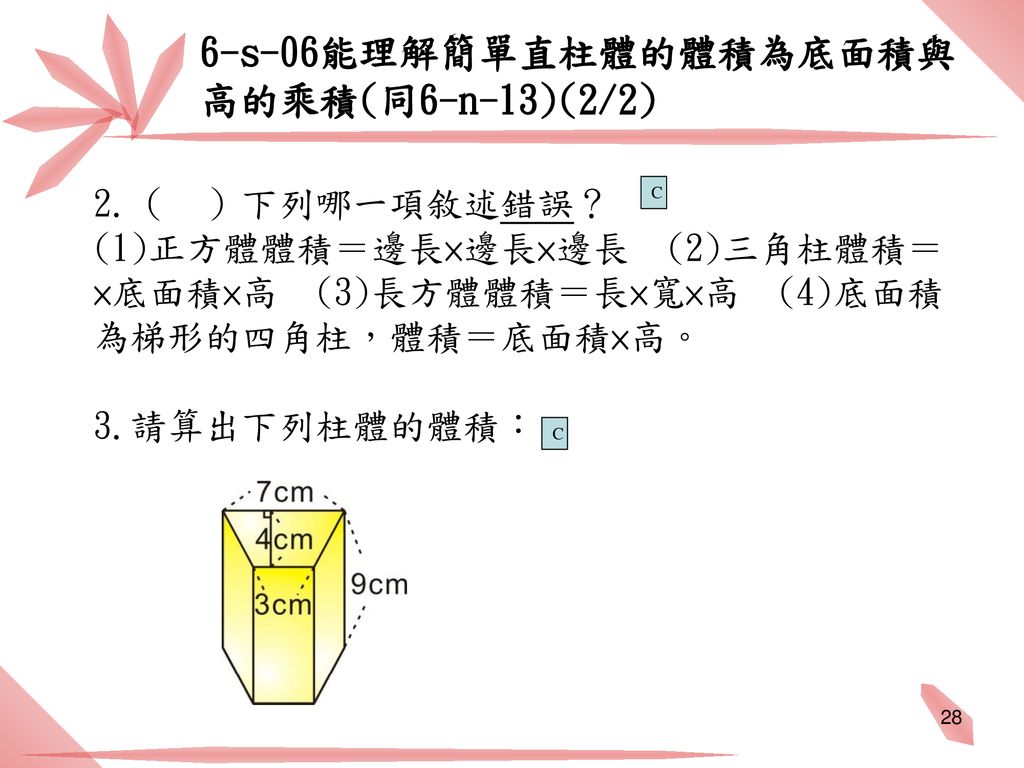



立體圖形 授課篇 適用年級 5 6年級設計者 Mri團隊 Ppt Download



正四角柱 正圓柱體




角柱の体積 Youtube




四角柱 Wikiwand



大嘴鳥親子雜誌



Q Tbn And9gcryo9hjyuw4rmo9g3nr2gckmswbtlowyo75xph7nnc25xnax0ls Usqp Cau




正四棱锥的表面积 正四棱锥体积和表面积计算公式 谢谢 三人行教育网 Www 3rxing Org



Www Sdime Ntnu Edu Tw Uploads Asset Data 5dfad41c E9 96 B1 E8 Ae 80 E4 B9 9d E4 B8 8b E7 Ac Ac E4 Ba 8c E7 Ab A0 E5 85 A8 Pdf
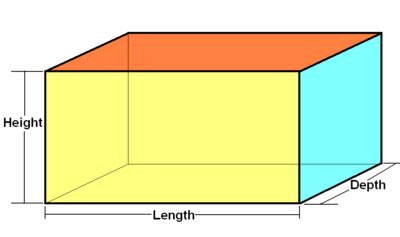



四角柱 Wikiwand
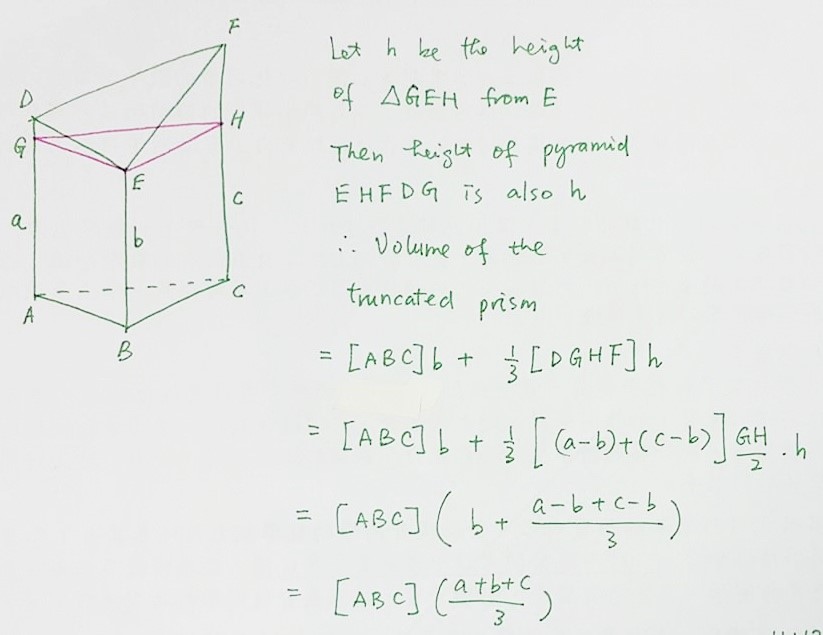



鈄截柱體體積 Quod Erat Demonstrandum



大嘴鳥親子雜誌




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




角錐體積公式的由來 Youtube




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ
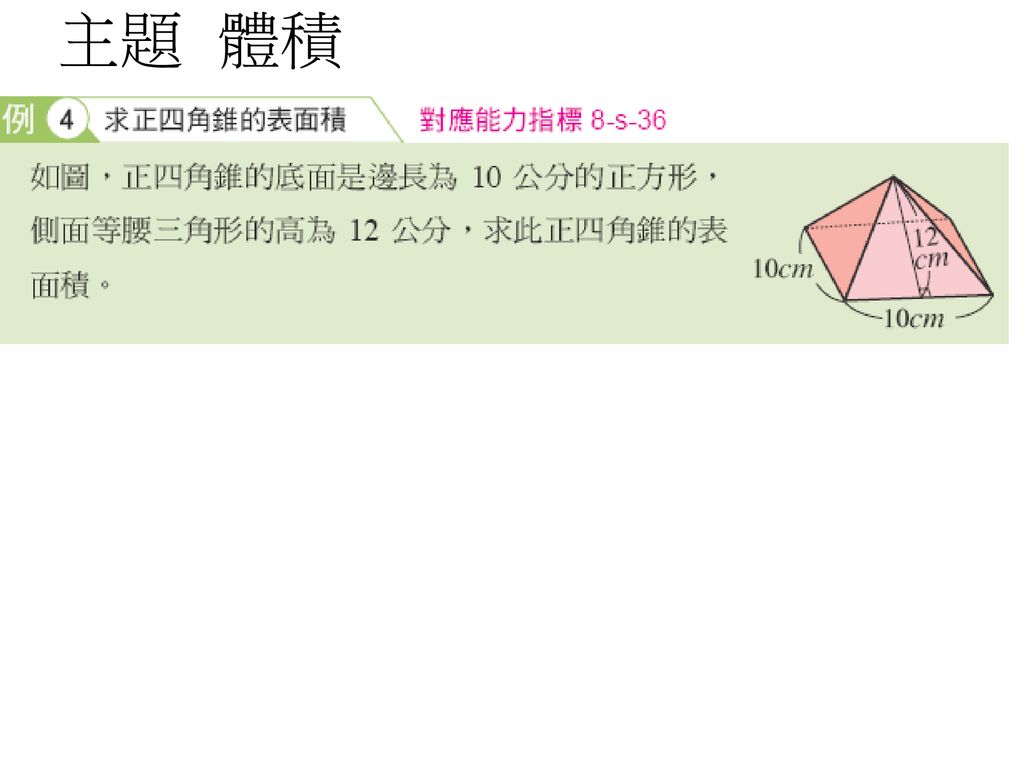



2 4 生活中的立體圖形能以最少性質辨認立體圖形 能理解柱體 錐體的頂點 面 邊的組合因素 能理解柱體 錐體的基本展開圖 Ppt Download




体積の求め方 計算公式一覧




鈄截柱體體積 Quod Erat Demonstrandum
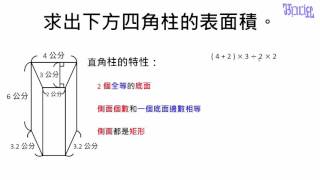



柱體的體積與表面積 04 求出四角柱的表面積 Youtube




Physics Quod Erat Demonstrandum




中2の数学で単項式の乗法と除法の範囲です 質問は Clear



1



Http Www Gjjh Tp Edu Tw Mediafile Fdownload 69 446 16 2 29 22 0 43 446 Nf1 Pdf




正四稜柱 上 下底面都是正方形 且側棱垂直於底面的稜柱叫做正四稜柱 正四 百科知識中文網




正四角柱から正四角錐へ Geogebra




四角柱 全世界条目




1 Boy的聲音問 Ppt Download




六角錐六角錐數 Yzkgo




梯形體積公式梯形體的體積計算公式 百度知道翻譯此網頁 Qbxfp




四稜柱 在幾何學中 四角柱又稱四稜柱 是指底面為四邊形的柱體 當底面為正 百科知識中文網




四角柱 维基百科 自由的百科全书



0 件のコメント:
コメントを投稿