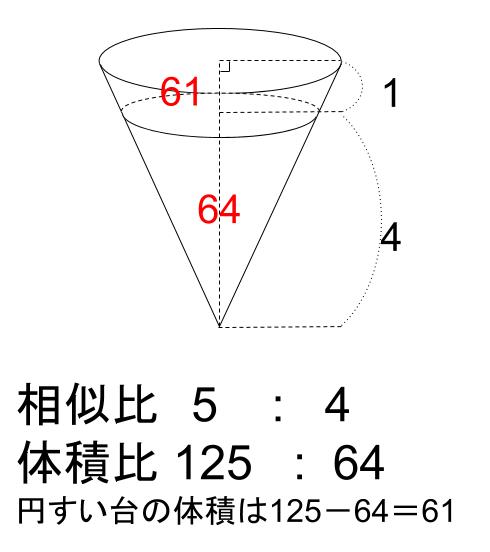
中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su
三種類の公式 0：13 まずは立体の体積を求める公式を確認しましょう。 角柱・円柱 底面積 × 高さ 角錐・円錐 底面積 × 高さ × 1 3 球 4 3 × π × r 3 3 種類の公式を使い、いろいろな立体の体積を求めてみましょう。立体の体積＆容積及び諸数値 立方体・直方体・円錐・角錐・球・円柱・六角柱・角柱 光正株式会社 役立つ資料シリーズ 立体の体積＆容積および諸数値 V=容積、S=表面積、As=側面積、Ab=底面積、x=底面より重心までの距離
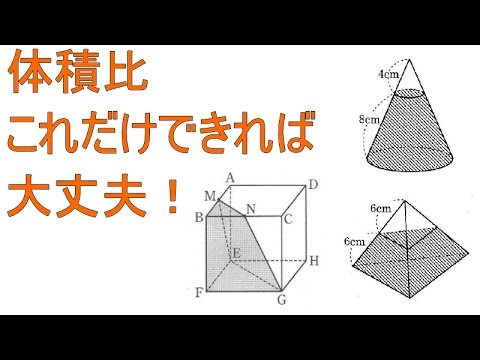
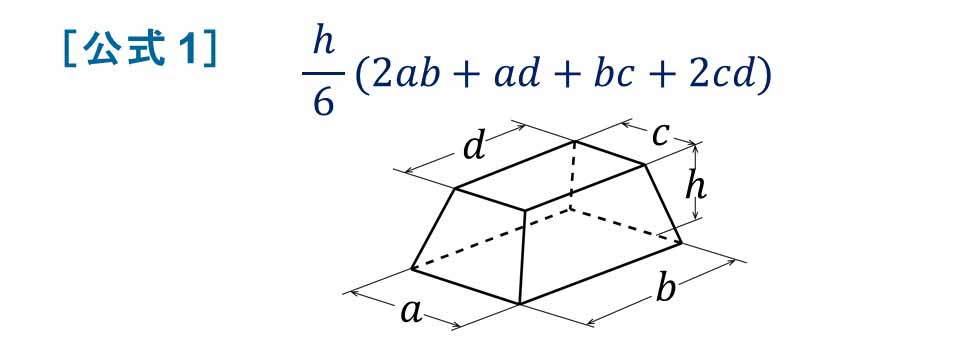
台形 体積 求め方 四辺の長さが違う
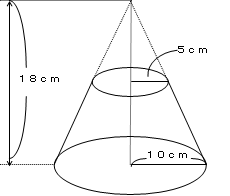
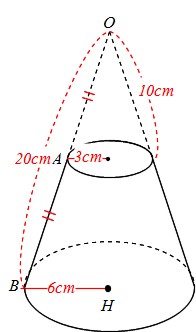
台形 体積 求め方 四辺の長さが違う- 1 回答 円錐台の体積を計算する方法を教えてください。 上面の数値と高さと角度がわかっている場合の体積の求め方を教えてください。 上面直径が05cm高さが5cm角度が2°の場合の円錐台。 cm3 (立方センチメートル)での答えの導き方を途中式を略さずに正しい公式は （a＋b＋√ab）×h÷3 です。 円錐台の体積の求め方は、底面積aの円錐の体積－底面積bの円錐の体積です。 単純に（a＋b）の半分の円柱にするのでは、円錐の性質上おかしなことが出てくるからです。 まず、切りとった円錐の高さlを求めます
また来てね問題集 図形問題 解答と解説 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん
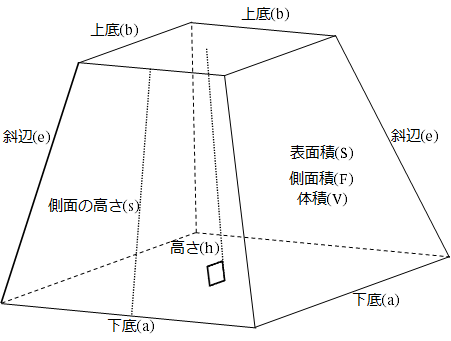
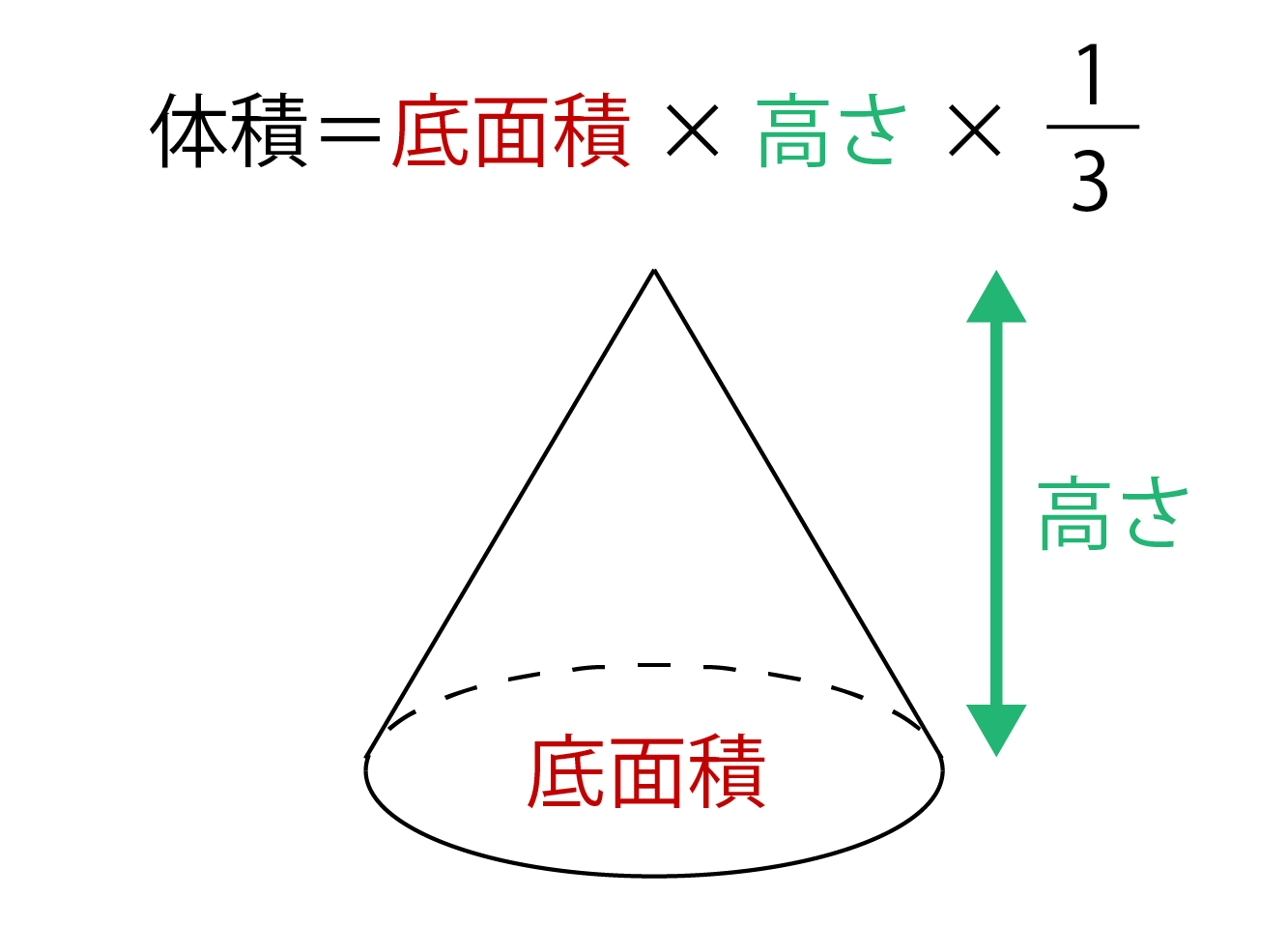
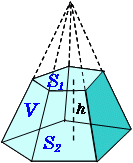
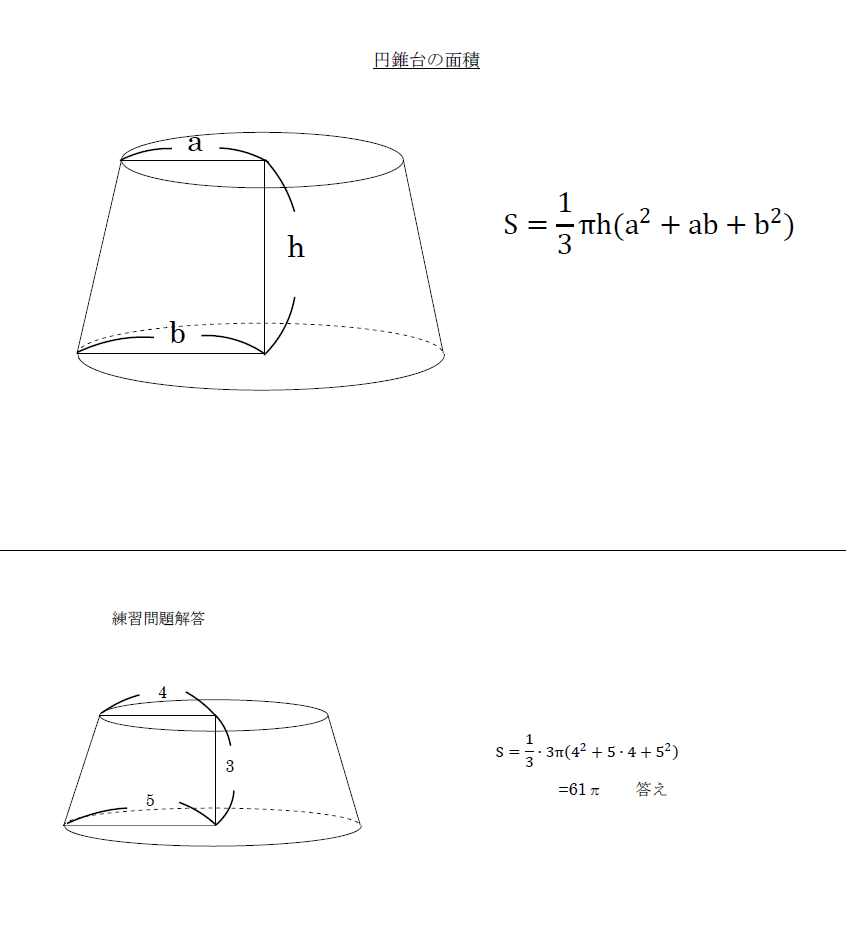
の体積は、底面積 S S 、高さ h h として、次の式で求められます。 この公式は、底面の形によりません。 錐体 すいたい の体積 V = 1 3Sh V = 1 3 S h 体積 = 底面積 × 高さ ÷ 3 角錐 かくすい と 円錐 えんすい の図を、それぞれ見てみましょう。 角錐の体積 底面積 S、高さ h の 三角錐 さんかくすい 三角錐や四角錐などの体積は、底面積 S S 、高さ h h として、次の式で求められます。 角錐 かくすい の円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S = π ( a b) ( a − b) 2 h 2 π ( a 2 b 2) 目次 計算ツール 円錐台の体積 円錐台の側面積 円錐台の表面積 計算ツール 大きな円錐の上側を 円錐は展開図にすると，円と扇形に分離されるのでこのような公式になります． 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います． 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて，次は円錐の体積を求める公式です．
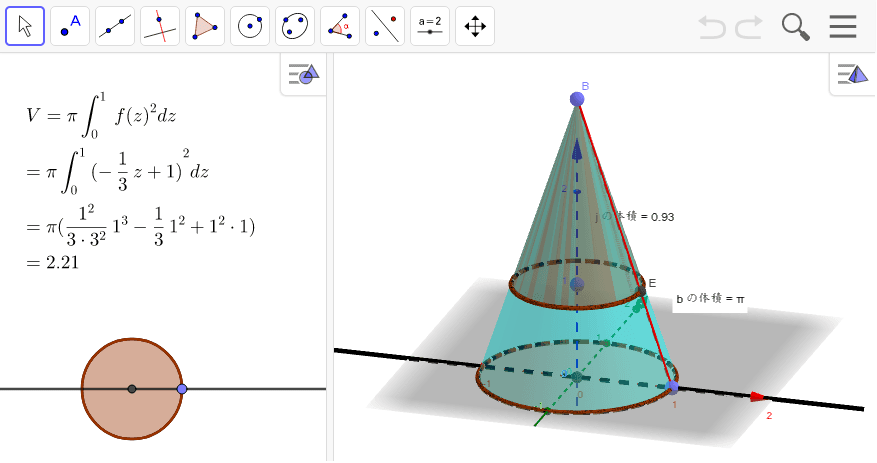
座標系の選び方 まず座標系を選びましょう。頂点を下側にすると計算が楽です。 微小な円盤の集合と見て体積を計算する 円錐の体積を計算するには、円錐を微小な厚さの円盤の集合と見立てて計算します。 微小な厚さの円盤の体積を\(\Delta V\)とすると小さい円錐と土台部分の体積比は？ という問いの答えは このように と求めてやることができました。 円錐を切り取って体積比を考えるような問題では 比較する立体が相似でなくても このように相似な立体を見つけて、不要な部分を取り除いたりし 定積分で体積を求める ある曲線下の面積を定積分で求められたように、ある平面を積み重ねてできる立体の体積も、定積分で求められます。 このとき、平面の積み重ね方には大きく分けて次の \(2\) 通りがあります。 平面を垂直に積み重ねる;
台形 体積 求め方 四辺の長さが違うのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 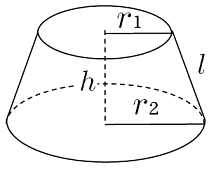 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 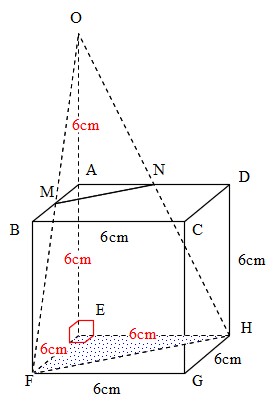 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |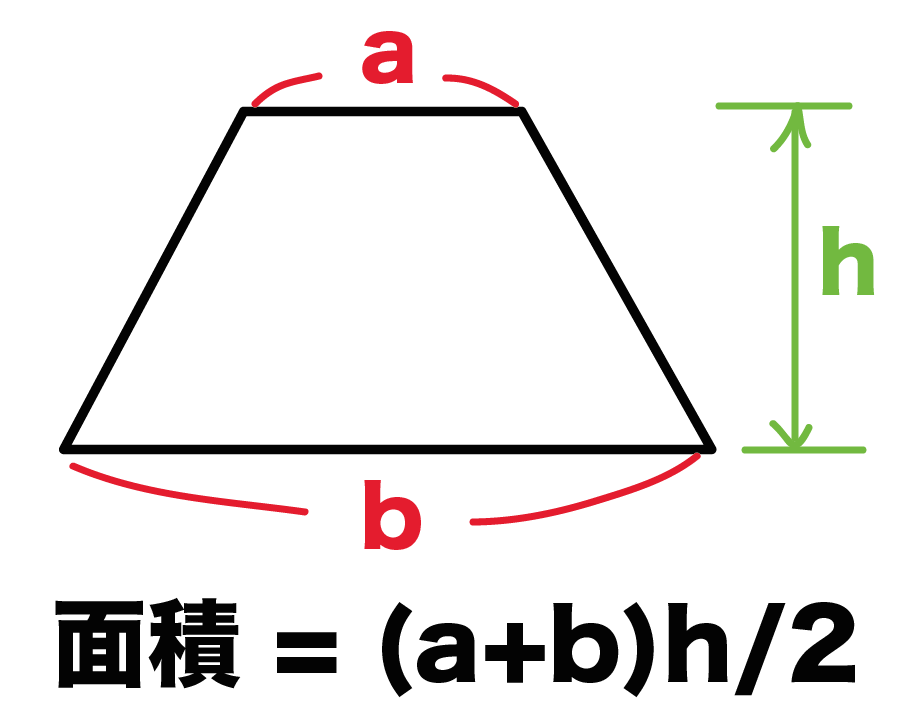
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 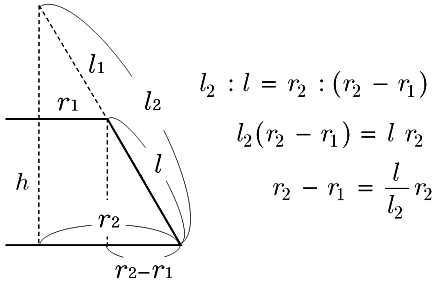 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 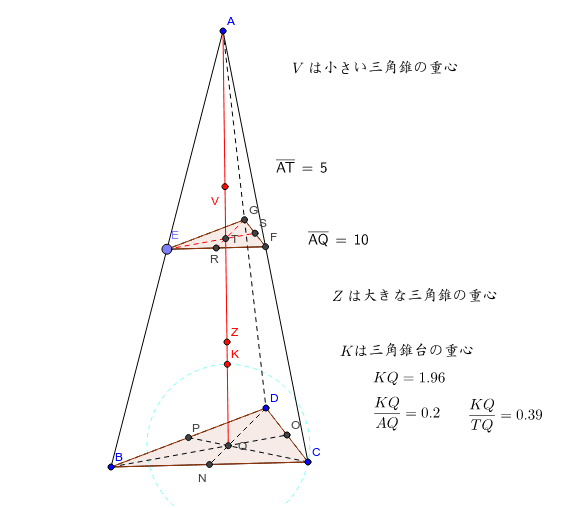 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |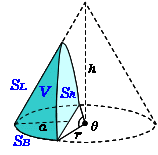
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |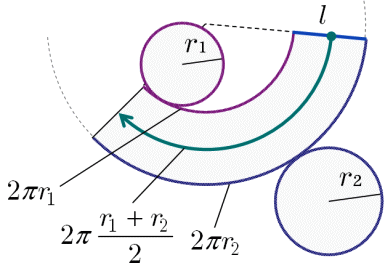
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 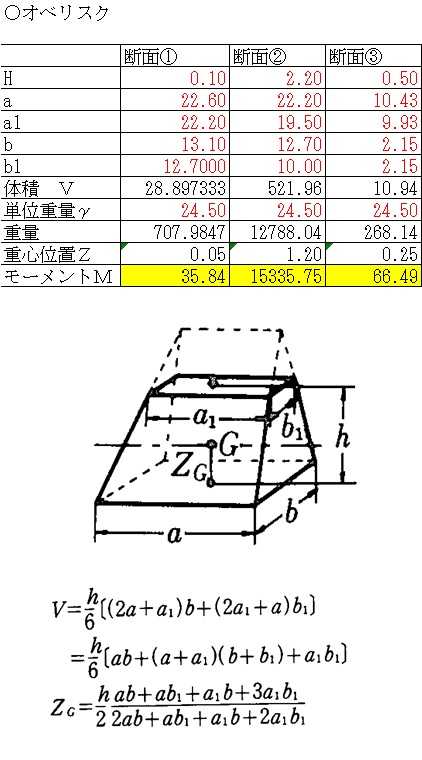 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |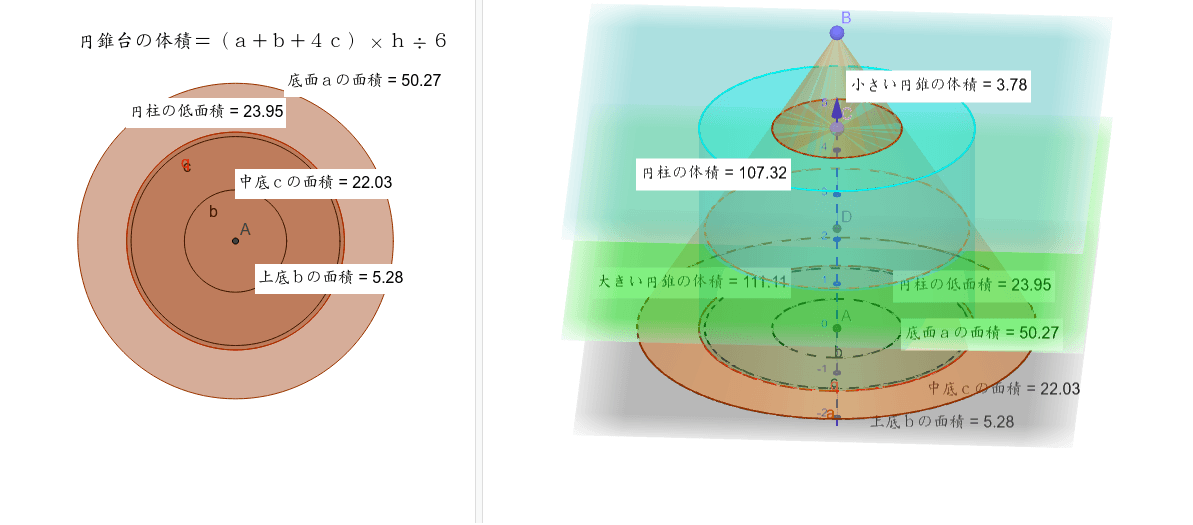
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 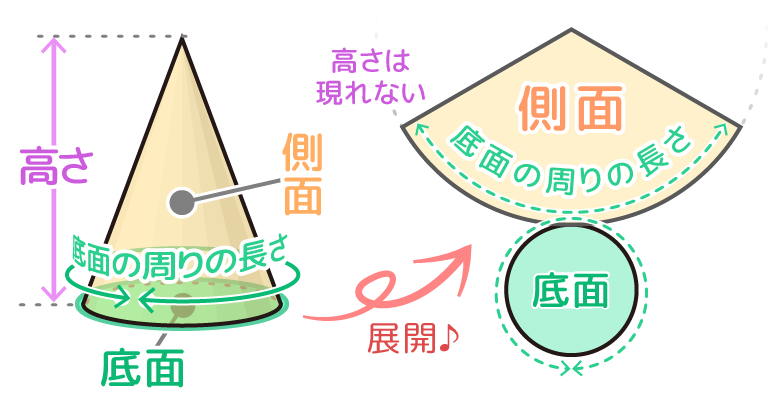 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |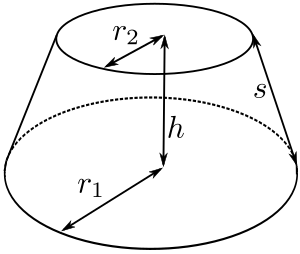
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |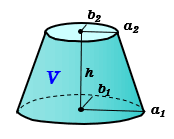
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 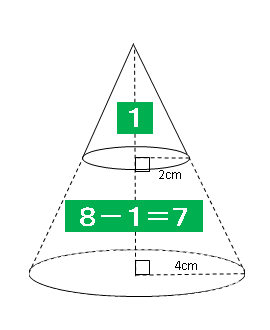 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |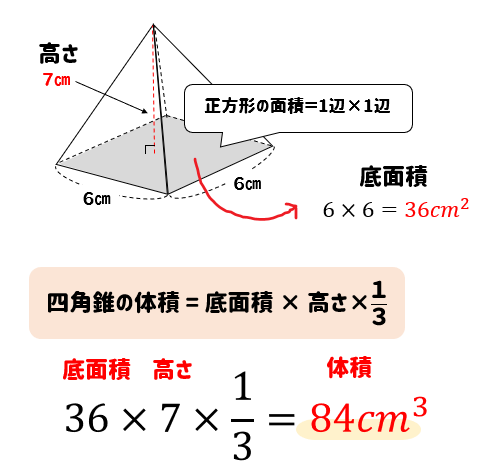
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 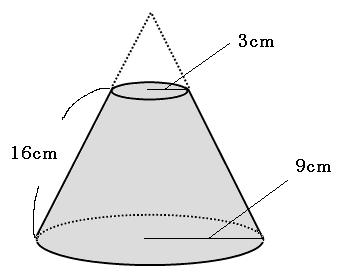 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 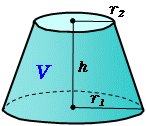 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 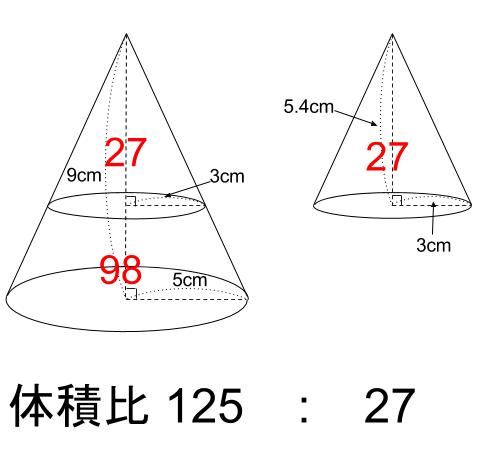 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
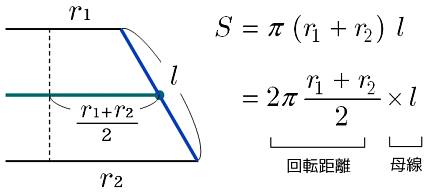 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 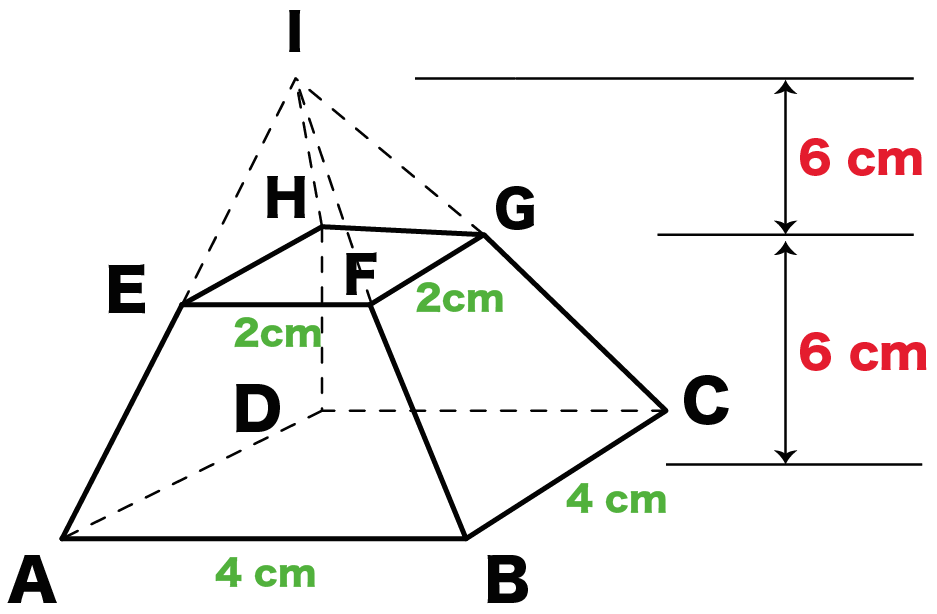 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 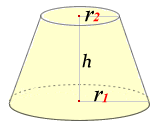 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 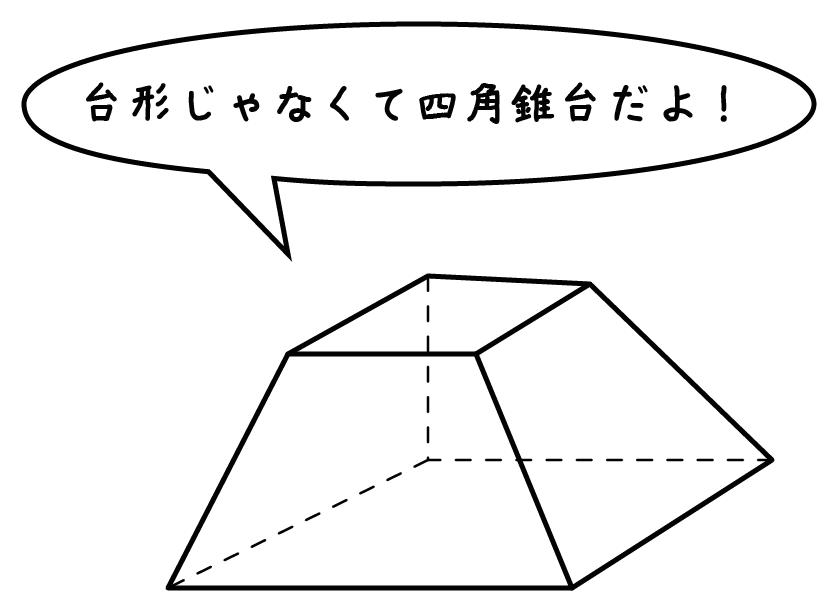 初等幾何 円錐台の側面積を求める 大人が学び直す数学 | 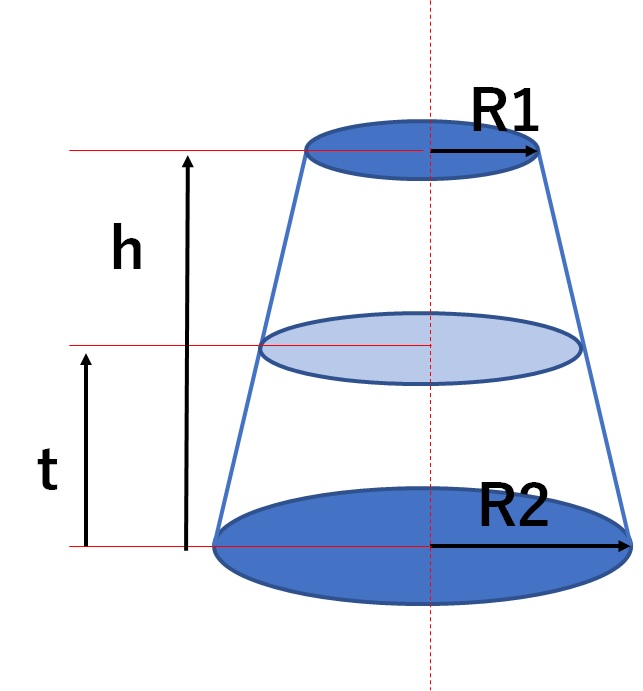 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
 初等幾何 円錐台の側面積を求める 大人が学び直す数学 |  初等幾何 円錐台の側面積を求める 大人が学び直す数学 |
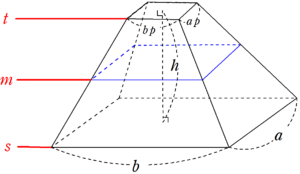
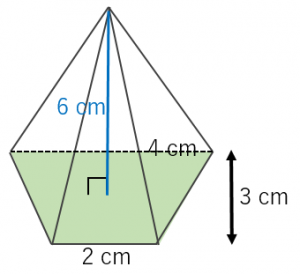
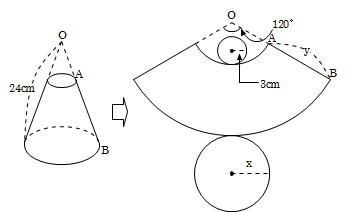
体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、 {（下の辺）×（下の辺） （下の辺）×（上の辺） (上の辺) × (上の辺) }×高さ÷3 ってことさ。 たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ！しかし円錐の場合、側面は扇形となりますが中心角は問題文で与えられないので少し複雑です。 なので円錐の側面積についてもう少し解説していきます。 円錐の側面積の求め方 側面積は扇形なので、扇形の面積の公式を書き出しましょう。
Incoming Term: 中1 数学 円錐 表面積の求め方, 台形の面積の 求め 方 いろいろ, 円錐 体積 3分の1 理由 小学生, 台形 体積 求め方 四辺の長さが違う, 球の体積 表面積 公式 覚え方, 球 円柱 共通部分 体積 重積分, 中1 数学 体積 表面積 公式 pdf, 面積 体積 公式 一覧 小学生, 角錐 体積 3分の1 理由 小学生, 中1数学 体積と表面積 問題 無料,
0 件のコメント:
コメントを投稿